In my last post, we saw how taking apart an area in different ways can lead to interesting results.  Let’s do that again.

Here is the square with length (a + b):

(When we looked at binomial squares, I used x and y.  This time, I’m using a and b.  You’ll see why soon.)

Below, I have broken up the square two different ways.  On the left, you see the familiar shapes that we used to derive the formula for the square of a binomial.  And on the right, you see a square surrounded by four identical right triangles.

This gives us two different ways to express the same area.  On the left, we have:

Area = (a + b)² = a² + 2ab + b²

On the right, we have one tilted square in the middle with side c, and 4 right triangles, each with a and b as their base and height.  We can add up their areas to find:

Area = (a + b)² = c² + 4 × ½ × a × b = c² + 2ab

But those two areas are equal.  They are two different ways of chopping up the same square.  That means…

a² + 2ab + b² = c² + 2ab

And if we subtract 2ab from both sides, we get a pretty well known result.

                           a² + b² = c²

where a and b are the legs and c is the hypotenuse  of a right triangle.

We use that theorem all the time.  Again, better with pictures.

All of these posts have been about using pictures to get an improved understanding of what the algebra is telling us.  These are ideas that I have been kicking around for a while so I thought I would share.  But they are leading up to something I’ll write about in the next post.  And I’ll reveal what got me started down this path again this year.

…of two squares.

Suppose we start with a square with side x and remove a smaller square with side y.

The remaining area (shown in blue) is literally “the difference of two squares”.

We can find its area by subtracting the little square from the big one to get:

Area = x² – y²

But we can also find the area another way.  Let’s cut things up and move them around.

As you can see, the area we were looking for is also the area of a rectangle.  The length is (x + y) and the width is (x – y).  That gives us a new formula for this area:

Area = (x + y)(x – y)

But we are talking about the same area both times.  So what we have now is a geometric reason to believe that the difference of two squares can be factored:

                                               x² – y² = (x + y)(x – y)

How important is this?  Hmm.  Within the context of high school math (and SAT math), it is apparently one of the most important factoring facts that there is.  In physics class, I can only think of one setting where we used this. (We were deriving a rule about velocities before and after an elastic collision, in case you were wondering.)

The math we teach should either be useful or interesting.  To me, the difference of two squares is more interesting when we use pictures.  And the idea of carving up the same area two different ways to see what you learn can be very powerful and lead to unquestionably important results.  More about this in the next post.

Well, I hope that the pictures in my last post changed the way you look at the square of a binomial.  And I am sure that I know what you are thinking now:

“What about binomials, cubed?”

We can figure this out algebraically. You may be inspired to see that:

(x + y)³ = (x + y)(x + y)² = (x + y)(x² + 2xy + y²)

And then we distribute:

(x + y)(x² + 2xy + y²) =

                   x(x² + 2xy + y²) +  y(x² + 2xy + y²) =

                                        x³ +2x²y + xy² + x²y + 2xy² + y³

And then you group the common terms to discover the rule for the cube of a binomial.

(x + y)³ = x³ + 3x²y +  3xy² + y³

Let me just say that you have a rare appreciation for algebra if that equation by itself stirs you.  And I would not be shocked to find that you skipped over the algebra that led to it.   But once again, it’s better with pictures.

This time, we build a cube with each edge x + y units long:

Then, we take that cube apart and see what we have:

Let’s take inventory.  The big cube we started with has been broken up into the following collection:

• A white cube with edge length x and volume x³
• A red cube with edge length y and volume y³
• 3 green rectangular slabs, dimensions x by x by y, with volume x²y
• 3 skinny blue rectangular solids, dimensions y by y by x, with volume xy²

But the volume of the collection has to add up to the volume of the big cube we started with.

That means:  (x + y)³ = x³ + 3x²y +  3xy² + y³ ! 

The 3-d picture makes this equation worthy of an exclamation point. The picture helps you to “see” the equation.  That can also work the other way around.  Let’s consider a 4-dimensional “hypercube” with edges that are (x + y).  I can’t picture those.  But I can still get some insight about them from the algebraic approach.  I’ll skip the steps this time and go right to the result:

(x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

Even though I can’t picture a 4-dimensional cube, I think I know what happens when you break it into pieces: you get 1 big hypercube, 1 smaller hyper cube and a variety of hyper-rectangular solids.  You can predict the dimensions and the number of each type from the equation above.  So I guess this time, it’s better with equations.

(The graphics in this post were created in Google Sketch-up by my daughter.)

Let’s start with a silly question about math vocabulary:

Why do some powers have special names?

The expression “ 3⁵ ” means “multiply 3 by itself 5 times”:   3⁵=3×3×3×3×3.  I’m not really worried about how to calculate this right now.  I just want to agree that we call it “three to the fifth”.   And raising to the fifth power doesn’t have any other special name.

And when we talk about x⁷ , we say “x to the seventh”.  Again, no special name.

But there are two powers that have additional names.  When we talk about say, 5², we most often call it “5 squared”.    Raising to the second power is called “squaring”.  Raising to the third power is called “cubing”.  And , of course, you knew that.   But it is easy to overlook why these (and only these) powers have these additional names.  The additional names have geometric meaning.

• When you raise a number to the second power, you are calculating the area of the square with a side of that length.  So we call it “squaring”.
• When you raise a number to the third power, you are calculating the volume of the cube with an edge of that length.  So we call it “cubing”.
• If we lived in 4 spatial dimensions, I bet we would have a name for raising things to the fourth power as well.

It is easy to overlook the geometric meanings of squaring and cubing.  I know this because of how my students respond when we talk about FOIL-ing to square a binomial.  The geometric meaning always seems to catch them by surprise.  But it is usually a happy discovery.

 CURSES! FOILed  AGAIN

For those of you who haven’t seen it in a while, I’ll review.  FOIL is a mnemonic device used to help students remember how to multiply binomials.  It is the result of distributing multiplication over addition multiple times.  You can use it to square binomials.

You start with an expression such as: (x + y)²

You re-write it:  (x + y)(x + y)  

Now, think of that first term as the multiplier and think of the second term as the sum over which multiplication is distributed.  You get:

(x + y)x + (x + y)y

Then you can distribute each of those as well.  That leads you to: x² + xy + xy + y²

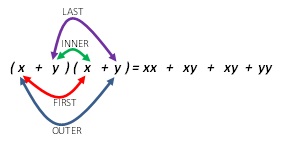
Before we combine the middle two terms, note that there are 4 pairings.  That’s where the mnemonic FOIL comes in.  You get the pairs by multiplying the FIRST terms, the OUTER terms, the INNER terms and the LAST terms.

I don’t have a problem with this mnemonic itself.  It’s kind of robotic, but I understand that you have to make certain processes automatic so that you can get to the next step.  I wouldn’t want my students to have to go back to the distribution property every time they see (x + y)².   In fact, I don’t want them to have to foil it either.  I want them to know that (x + y)² = x² + 2xy + y² not because they have memorized it but rather because they can picture it!

THE GEOMETRIC MEANING OF (x + y)²

We call it “squaring” because it gives us the area of the square.

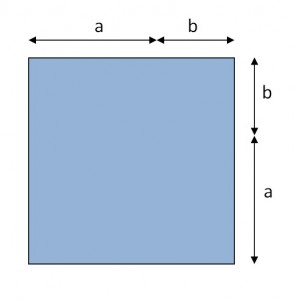
So (x + y)² is the area of the square with length (x + y).  Now, let’s draw some pictures.

Here is a line segment with a length of x + y:

And here is the square with a side that has that same length:

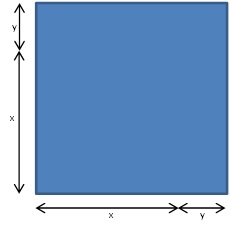
The area of that square is certainly (x + y)².

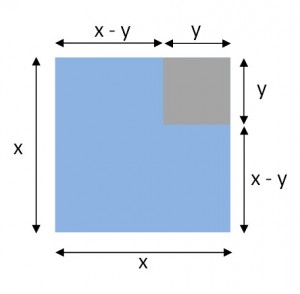
But what if we break that square into smaller regions?

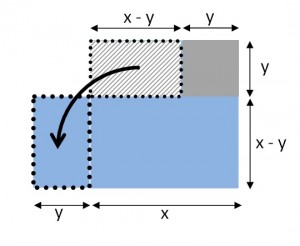
The picture tells the story in a more intuitive and memorable way than foiling ever could.  We are clearly looking at a big square (with area = x²), a little square (with area = y²), and two identical rectangles (each with area = xy).  This is the diagram that goes with the rule for binomial squares:

(x + y)² = x² + 2xy + y²

But it’s better with pictures.

Next post — higher dimensions.

And then x² – y².   Spoiler: it really is the difference of two squares.

My name is Philip Keller.  I teach physics at Holmdel High School in New Jersey.  My students are fine young men and women who patiently indulge (and even encourage) my occasional digressions on to topics that, while physics-related, are not officially in our curriculum.  When I can, I like to show them other ways of looking at the math they already know.  Or show them the math that they should have known before taking on the challenge of learning physics.

Some of these topics are gathered and organized in a book that I hope to release this summer.  Advanced Math for Young Students: A First Course in Algebra is designed for middle school students to give them a head start in thinking algebraically and using algebra to solve puzzles and to express relationships.  That’s what we do in physics all the time.

Working on this project has led me to ponder other mathematical questions that are more suitable for high school students and teachers to ponder.  I would like to use this blog to explore some of them as well.  Expect a mixture of math, physics and some ideas about how we teach them.

I am new to blogging in general and to WordPress in particular.  As I learn its features, expect format changes and all kinds of plug-ins and gizmos.  I expect to eventually settle down to a consistent look, but for now there are so many new toys to play with.

Mr K