So how are areas related to antiderivatives? In other words (and symbols):
This is the fundamental question. When you know the answer, you will know the “Fundamental Theorem of Integral Calculus”. But the main idea behind this all is something you have seen before in physics class (but not used quite this way).
In your first physics class, while studying kinematics, you learned that the area under a velocity vs time graph tells us the change in the object’s position. To help jog your memory, play the video below:
The upper graph shows the velocity as a function of time for an object that happened to have a constant velocity of 10 m/s.
The lower graph shows the position vs time for the same object. The velocity is constant so the position graph is linear with a constant slope.
On the velocity graph, you can see the area being swept out from t = 3 s to t = 7 s. And on the position graph, you can see how far the object has moved during the same time interval. Try stopping the animation at different times. Examine the graphs until you have convinced yourself of the following claim:
For a given time interval, the area under the Velocity vs. time graph will be equal to the change in position during that time interval.
YOU MAY BE SKEPTICAL…
After all, that was just with constant velocity. But what if the velocity is changing? Like so…
The velocity is increasing linearly and the position is increasing quadratically. [Remember, velocity is the derivative of position with respect to time. And the derivative of a 2nd-degree polynomial is a linear function.]
But even so, once again we see:
For a given time interval, the area under the Velocity vs. time graph will be equal to the change in position during that time interval.
STILL SKEPTICAL? STAY TUNED…
The velocity does not have to be changing linearly. In fact, it does not even have to be velocity and position that we are talking about. It can be any two quantities where one is the derivative of the other. Here’s one where the first graph is the rate at which water flows into a container and the second graph is the volume of water in that container:
Stop the animation at various points to check our claim:
If f(x) is the derivative of F(x), then the area under the graph of f(x) is equal to the change in F(x) over that same interval.
When we used this in 1st-year physics, we were using the area under the DERIVATIVE (velocity vs time) to find the change in the original function (position vs. time). But now that we know how to find anti-derivatives, we can do this the other way around, using the change in the ANTI-DERIVATIVE (position) to find the area under the graph of the original function (velocity vs time).
And that answers the question we started with. What does area have to do with antiderivatives? The area under the graph is equal to the change in the antiderivative. That is called the Fundamental Theorem. We write:
WHY IS THIS USEFUL?
Well, suppose you want to find the area under some graph. This theorem gives you a procedure you can follow:
Step 1: Find an antiderivative.
Step 2. See how much the antiderivative changed by over the interval.
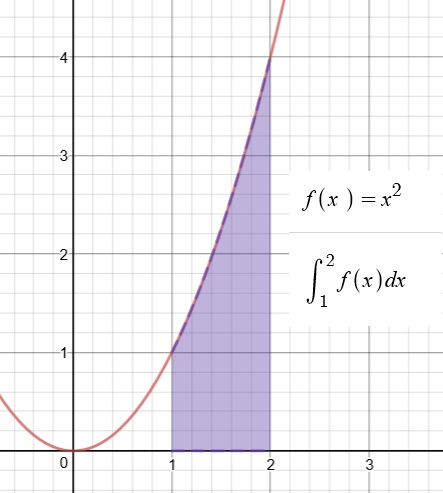
For example, suppose we want to know the area under the graph of f(x)=x2 between x=1 and x = 2, as illustrated below.
Let’s see. Can we find an antiderivative? Oh, yes, this one we did already.
F(x)=(1/3)x3 is an antiderivative of f(x)=x2.
So now we just have to see how much F(x) has changed over the interval from x = 1 to x = 2.
F(3) = (1/3)(2)3 = 8/3
F(1) = (1/3)(1)3 = 1/3
F(3) – F(1) = 7/3
But what if I can’t find the antiderivative?
Well, that could be a problem. That’s why you will spend so much time developing this skill in AP Calculus. But I will reassure you again: in AP Physics, the antiderivatives you need will be manageable. And there’s always Wolfram Alpha…
Wait! I don’t really understand how you can calculate the area of something with curvy boundaries. What does that even mean?
And I don’t understand: why does the area under the velocity graph equal the displacement? Do we just have to accept that?
And I still don’t see why this is so important? Are there lots of areas to be found in AP Physics?
These questions turn out to all be related! See next post, Part III of our discussion of areas and integrals.