…to Complete a Square
As you have seen, quadratic equations can pop up unexpectedly. Here’s one:
x2 + 4x – 12 = 0
I chose this one because it does “factor”, but I don’t want to solve it that way. Factoring causes stress. When you have not yet found the factors, you start to wonder:
Is it just me? Or does this thing have no factors?
When you are ready to give up, you turn to the quadratic formula. To solve:
ax2 + bx + c = 0
you just have to identify the values of a, b and c and then plug them into the magic formula:
For our example, a=1, b=4 and c= -12. So we get:
But you have to admit, there’s something mindless and robot-like about solving quadratics this way. It’s like we are impersonating a computer. If you are going to be mindless, you might as well use the solve function on a TI-89 and be done with it. But there is another alternative. We could go back to the algorithm that the quadratic formula is derived from. It’s clever and it has style. And even better, it has diagrams!
COMPLETING THE SQUARE
Let’s start again with:
x2 + 4x – 12 = 0
And re-write it:
x2 + 4x = 12
And one more time:
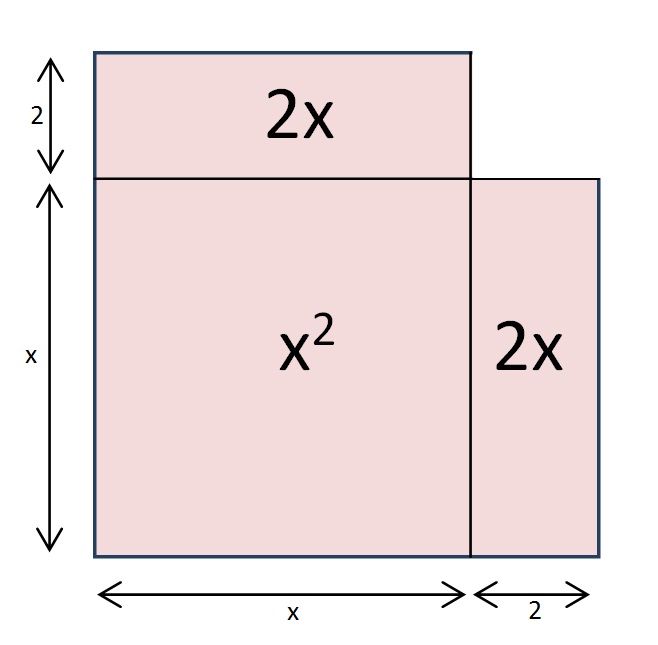
x2 + 2x +2x = 12
But why do this? Well, the left side of that equation has a nice picture that goes with it:
It’s ALMOST a square. And if we add one little square…
We have just “completed the square”!
By adding that little blue square, we have made a bigger square with a side of length (x+2).
But that addition would leave our original equation out of balance. So if we add 22 to one side, we also have to add it to the other side:
x2 + 2x +2x + 4 = 12 + 4
As you can see from the picture, the left side of our equation is now a perfect square. That means that we can write:
(x + 2)2 = 16
We can solve this pretty quickly. Take the square root of both sides to get:
(x + 2) = ±4
x= -4 – 2 = -6 or 4 – 2 = 2
Q: Isn’t factoring faster?
A: It is when it is. But when it isn’t, it really isn’t. And completing the square works either way.
For example, here’s one that doesn’t factor:
x2 + 5x – 4 = 0
x2 + 2.5x +2.5x = 4
x2 + 2.5x +2.5x + 2.52= 4 + 2.52
(x + 2.5)2 = 10.25
You will still need a calculator if you want to tidy up, but you would have needed one had you used the quadratic formula instead.
OK, I am not expecting to win a lot of converts here. I just think that when you connect it with its diagrams, completing the square has an elegance to it that the quadratic formula lacks. (But if I had to do a whole page of these to do,say 1 – 99 odd, I would grab a TI-89 and move on.)
I have only seen one physics student use completing the square in class. She did it effortlessly with the same automaticity that most students bring to “cross-multiply and divide”. But she learned her algebra in another country.