Well, I hope that the pictures in my last post changed the way you look at the square of a binomial.  And I am sure that I know what you are thinking now:

“What about binomials, cubed?”

We can figure this out algebraically. You may be inspired to see that:

(x + y)³ = (x + y)(x + y)² = (x + y)(x² + 2xy + y²)

And then we distribute:

(x + y)(x² + 2xy + y²) =

                   x(x² + 2xy + y²) +  y(x² + 2xy + y²) =

                                        x³ +2x²y + xy² + x²y + 2xy² + y³

And then you group the common terms to discover the rule for the cube of a binomial.

(x + y)³ = x³ + 3x²y +  3xy² + y³

Let me just say that you have a rare appreciation for algebra if that equation by itself stirs you.  And I would not be shocked to find that you skipped over the algebra that led to it.   But once again, it’s better with pictures.

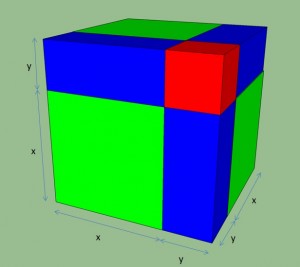
This time, we build a cube with each edge x + y units long:

Then, we take that cube apart and see what we have:

Let’s take inventory.  The big cube we started with has been broken up into the following collection:

• A white cube with edge length x and volume x³
• A red cube with edge length y and volume y³
• 3 green rectangular slabs, dimensions x by x by y, with volume x²y
• 3 skinny blue rectangular solids, dimensions y by y by x, with volume xy²

But the volume of the collection has to add up to the volume of the big cube we started with.

That means:  (x + y)³ = x³ + 3x²y +  3xy² + y³ ! 

The 3-d picture makes this equation worthy of an exclamation point. The picture helps you to “see” the equation.  That can also work the other way around.  Let’s consider a 4-dimensional “hypercube” with edges that are (x + y).  I can’t picture those.  But I can still get some insight about them from the algebraic approach.  I’ll skip the steps this time and go right to the result:

(x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

Even though I can’t picture a 4-dimensional cube, I think I know what happens when you break it into pieces: you get 1 big hypercube, 1 smaller hyper cube and a variety of hyper-rectangular solids.  You can predict the dimensions and the number of each type from the equation above.  So I guess this time, it’s better with equations.

(The graphics in this post were created in Google Sketch-up by my daughter.)