In my last post, I reported on the results of your hair-growing experiment.
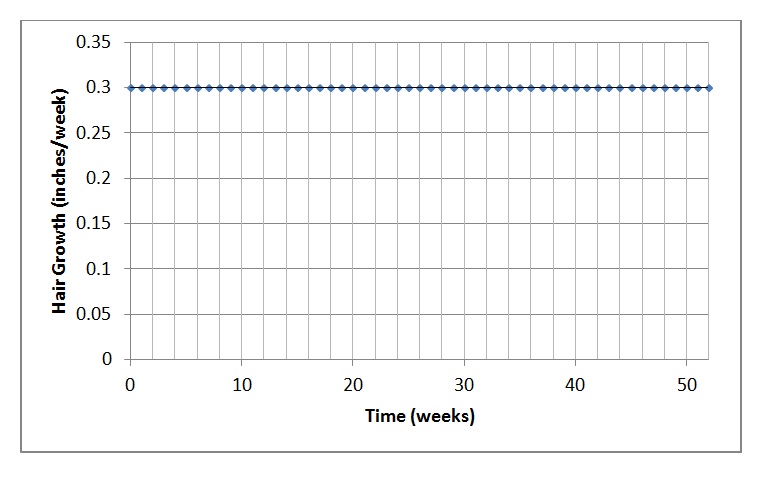
Now suppose that at the end of the year, you go back and analyze your year of hair growth. You can see from the graph that your hair grew steadily at a rate of 0.3 inches per week. That was the slope of the graph no matter what time interval you chose to examine. So we concluded that the rate was constant.
If we feel like it, instead of graphing hair length, we could graph the graph the growth rate instead.
This graph is not that exciting. Since your hair grew at the same rate week after week, this graph is a horizontal line. But it is important to understand that we are still talking about the same experiment. The first graph showed hair length. That graph slopes uphill at a constant rate. This new graph shows growth rate – it is the slope of the previous graph. And since that graph had a constant slope, this new graph is horizontal.
Now let’s suppose that you were not satisfied with the year’s hair growth. So you search the internet for hair growth accelerators. (I’m sure people actually do this.) And let’s also pretend that you find one that really works as advertised. It promises that if you use it every day, you will experience steadily increasing hair- growth-rates. In fact, they promise:
Guaranteed Acceleration = .023 inches/week2
Exactly what does this mean? If you are new to physics, it is possible that you don’t know how to interpret this guarantee. I mean, what is a “week squared” anyway?
Still, you decide to try it. In the interest of science, you shave off your hair on New Year’s Day and begin the experiment. Here are your results:
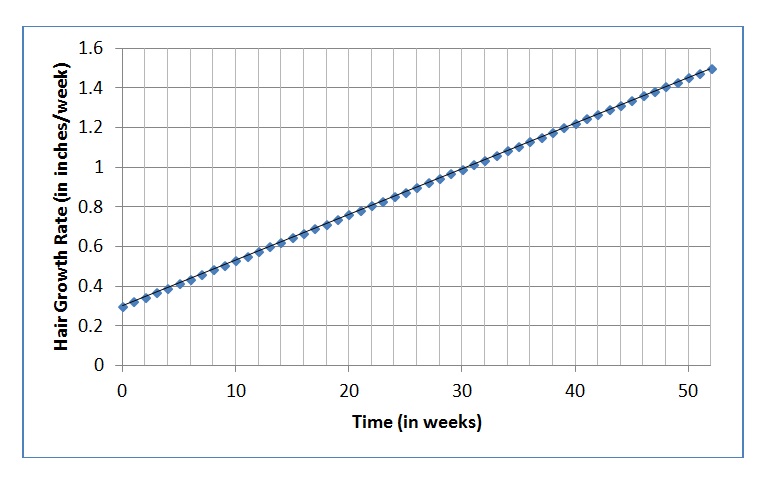
Now that’s some seriously long hair! In one year, your hair has grown nearly four feet! And when we look at the graph of growth rate, it is now a little more interesting:
Your rate of hair growth certainly increased. It was 0.3 inches per week at the beginning of the year. And by the end of the year, the rate had increased to 1.5 inches per week, increasing by 1.2 inches per week over the course of the year. But the increase did not happen all at once. The growth rate increased steadily.
By how much did the growth rate increase each week?
We can answer this question two different ways.
1. Since we know that the rate increase for the entire year was 1.2 inches per week, we can divide to find the weekly increase:
1.2 ÷ 52 ≈ .023 inches per week per week
Let’s make sure to understand what we just figured out. Each week, the growth rate increases by .023 inches per week. At the beginning of the year, the rate was .3 inches per week. After 1 week, it will have increased to .3 + .023 = .323 inches per week. After 2 weeks, it will increase and additional .023 inches per week to .3 + .023 +.023 = .346 inches per week. In other words:
Hair Growth Acceleration = .023 (inches/week)/week
When we are being lazy, we write: .023 inches/week2
2. We can also find the growth rate by evaluating the slope of the graph of growth rate. Just like hair “velocity” is the slope of the graph of hair length vs. time, hair acceleration is the slope of the velocity graph. And since that graph is linear, we can pick any two points to calculate the rise over run.
Using the points I have chosen, we get a rise of .6 inches per week over a run of 26 weeks which comes out to a slope of .6 ÷ 26 ≈ .023 (inches/week)/week, just as we expected.
But to even draw a graph like this, we must somehow believe that at any given moment in time, your hair is growing at some particular rate. So now let’s look back at the graph of hair length vs. time:
You can see that this graph is NOT linear. As time passes, the slope gets steeper because your hair growth is accelerating. Every instant, the rate is changing. Again, we seem to be talking about instantaneous growth rates. That’s our next topic.