Hello all…sorry the posts are coming at such long intervals.  I am teaching a new class this year — multivariable calculus! — and it is taking up lots of time as I try to remember/recreate/invent some level of understanding, having last taken the course 30 years ago.  But I am having a lot of fun with it, teaching a small group of fine (and patient) students, learning a lot.

And speaking of things that come at long intervals…here is a puzzle that was posted on 538.com in their new feature: “The Riddler”.  This was from week #2:

You arrive at the beautiful Three Geysers National Park. You read a placard explaining that the three eponymous geysers — creatively named A, B and C — erupt at intervals of precisely two hours, four hours and six hours, respectively. However, you just got there, so you have no idea how the three eruptions are staggered. Assuming they each started erupting at some independently random point in history, what are the probabilities that A, B and C, respectively, will be the first to erupt after your arrival?

The full post is at:  http://fivethirtyeight.com/features/which-geyser-gushes-first/

and a complete solution is in the next week’s post:

http://fivethirtyeight.com/features/how-long-will-your-smartphone-distract-you-from-family-dinner/

But what I want to discuss is a different way of thinking about the solution than the one posted at 538.  I want to use geometric probability.  [If you want to solve this on your own, spoilers ahead.]

Let’s start with an easier version of the question…

Suppose the only geysers were A and B.

If you have just arrived, Geyser A will erupt in x hours, where x is between 0 and 2. And Geyser B will erupt in y hours, where y is between 0 and 4.  Intuitively, it seems likely that y will be greater than x.  One way to see this is to use geometric probability.  Think of every possible outcome as an ordered pair.  Then, all possible outcomes can be represented as an area on the coordinate plane.  I used Desmos.com to graph the region and also the line y=x, or more precisely, the shaded half-plane y>x.

Geyser A will erupt first whenever y>x. So the probability we seek is the area of the part of the box above the x=y line divided by the total area of the box.  You can just about count boxes to determine that this occurs 6/8 (or 3/4) of the time.

OK then.  Now let’s bring Geyser C back into the problem…

From the moment you arrive, you know that Geyser C will erupt in z hours, where 0<z<6.  But you can still use geometric probability.  Each outcome can be thought of as an ordered triple (x,y,z).  The space of all outcomes is now a 2 x 4 x 6 rectangular solid.  And if you are looking for the probability that Geyser A erupts first, you want to slice that solid up with the planes x=y and x=z.

I don’t know if Desmos can do this kind of thing.  But fortunately, Paul Seeburger’s Multivariable Calculus Exploration applet can be used to visualize this problem.  You can find the applet here:

http://web.monroecc.edu/manila/webfiles/calcNSF/JavaCode/CalcPlot3D.htm

Note: on my computer, I can only open this page in Firefox.  YMMV.

Here is the solid that represents the set of all possible outcomes: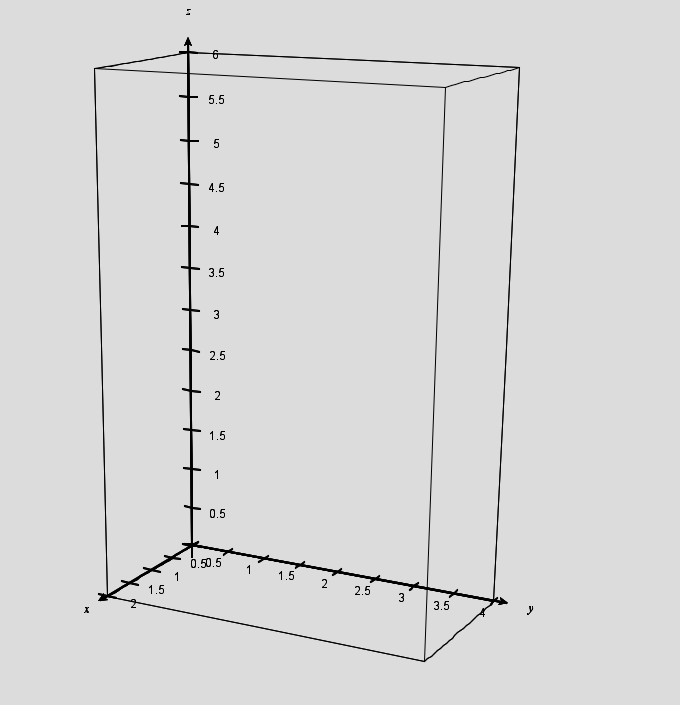

And here is that same solid, cut by the planes x=y and x=z:

We need to find the volume of the part of this box “to the right” of the x=y plane and “above” the x=z plane. It’s easier to see what we are looking for if you rotate the diagram to view it “from behind”:

In this diagram, the volume defined by points where y>x and z>x can be broken into four chunks.  I’ve added the x=2 plane and the z=2 plane to help you see them.

The rectangular solid on the upper left: V = 2x2x4=16

The triangular prism in the front on the lower left: V = (1/2)x2x2x2=4

The triangular prism in the front on the upper right: V = (1/2)x2x2x4 = 8

The front half of the pyramid on the bottom right: V = (1/3)(2)(2)(2) = 8/3

(If you are having trouble seeing the pyramid: in this view, we are looking through its 2×2 base, looking toward its vertex which is 2 units away.)

The probability of Geyser A erupting first is the sum of these volumes divided by the total volume of the box, or:

(16 + 4+ 8 + 8/3)/(2x4x6) which reduces to 23/36.

Using a similar method but with different cutting planes, you can find the pictures that will give you the probabilities of Geyser B or Geyser C erupting first.  And you do get the same answer that is posted on the Riddler’s webpage.

You can post questions (or ask me in class) if you need help with those last two…