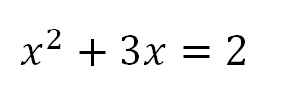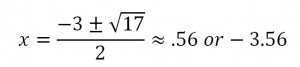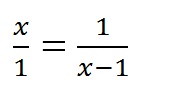…to Complete a Square

As you have seen, quadratic equations can pop up unexpectedly.  Here’s one:

x² + 4x – 12 = 0

I chose this one because it does “factor”, but I don’t want to solve it that way.  Factoring causes stress.  When you have not yet found the factors, you start to wonder:

Is it just me? Or does this thing have no factors? 

When you are ready to give up, you turn to the quadratic formula.  To solve:

ax² + bx + c = 0

you just have to identify the values of a, b and c and then plug them into the magic formula:

For our example, a=1, b=4 and c= -12.  So we get:

But you have to admit, there’s something mindless and robot-like about solving quadratics this way.  It’s like we are impersonating a computer.  If you are going to be mindless, you might as well use the solve function on a TI-89 and be done with it.  But there is another alternative.  We could go back to the algorithm that the quadratic formula is derived from.  It’s clever and it has style.  And even better, it has diagrams!

COMPLETING THE SQUARE

Let’s start again with:

x² + 4x – 12 = 0

And re-write it:

x² + 4x = 12

And one more time:

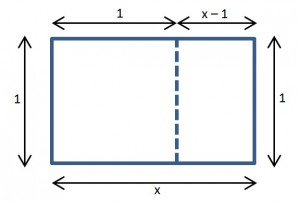
x² + 2x +2x = 12

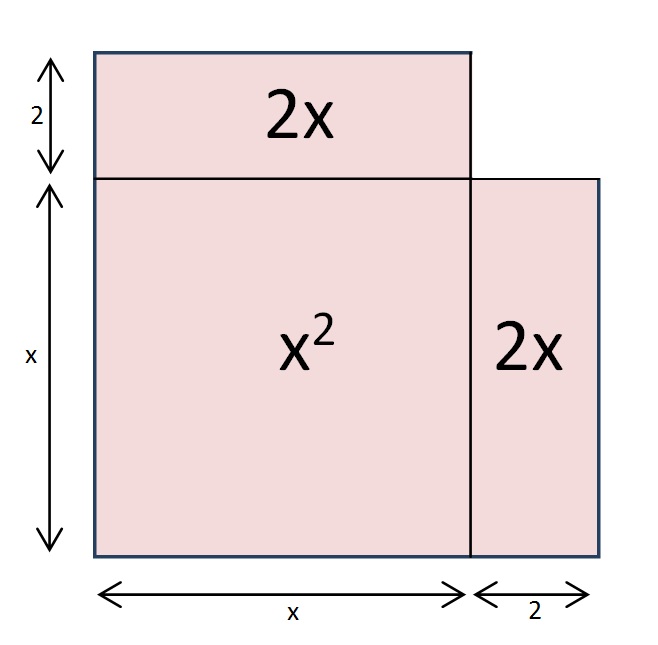
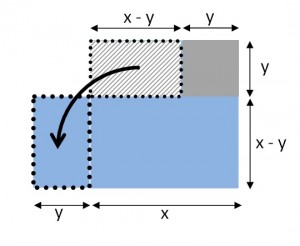
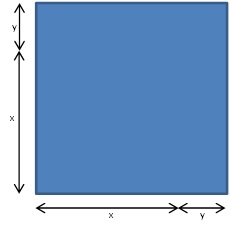
But why do this?  Well, the left side of that equation has a nice picture that goes with it:

It’s ALMOST a square.  And if we add one little square…

We have just “completed the square”!

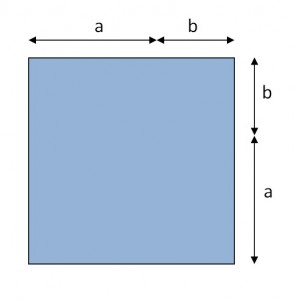
By adding that little blue square, we have made a bigger square with a side of length (x+2).

But that addition would leave our original equation out of balance.  So if we add 2² to one side, we also have to add it to the other side:

x² + 2x +2x + 4 = 12 + 4

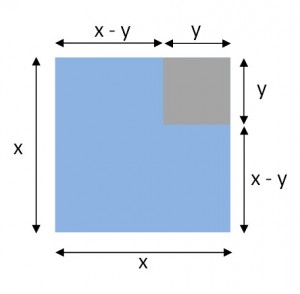
As you can see from the picture, the left side of our equation is now a perfect square. That means that we can write:

(x + 2)² = 16

We can solve this pretty quickly.  Take the square root of both sides to get:

(x + 2) = ±4

x= -4 – 2 = -6 or 4 – 2 = 2

Q: Isn’t factoring faster? 

A: It is when it is.  But when it isn’t, it really isn’t. And completing the square works either way.

 For example, here’s one that doesn’t factor:

x² + 5x – 4 = 0

x² + 2.5x +2.5x = 4

x² + 2.5x +2.5x + 2.5²= 4 + 2.5²

(x + 2.5)² = 10.25

You will still need a calculator if you want to tidy up, but you would have needed one had you used the quadratic formula instead.

OK, I am not expecting to win a lot of converts here.  I just think that when you connect it with its diagrams, completing the square has an elegance to it that the quadratic formula lacks.  (But if I had to do a whole page of these to do,say 1 – 99 odd, I would grab a TI-89 and move on.)

I have only seen one physics student use completing the square in class.  She did it effortlessly with the same automaticity that most students bring to “cross-multiply and divide”.  But she learned her algebra in another country.

Here is an interesting fraction to ponder:

Constructions such as these are called “continued fractions”. Though they go on forever, there is a way to evaluate them.  Before we do that, let’s get a feel for the answer we seek by figuring out an upper and lower limit on the value.

1.  x is less than 2/3.

We know this because the numerator is 2 and the denominator is 3 + something positive.  If the denominator is MORE than 3, then the fraction is LESS than 2/3.  But how much less?  Well, there is a limit on that as well…

2. x is more than 6/11.

As we just said, the denominator is more than 3, but how much more?  Look again at the “something positive” which is added to the denominator:  it is in fact the same expression x that we are hoping to find.  We don’t know its value, but we know it is less than 2/3.  So now we have:

The fraction will have its smallest value when the denominator is the biggest it can be.

That gives us a lower limit on the value of x:

But what if we want an exact value?  It turns out that we’ve already noticed the key to this puzzle.

Look again at the continued fraction.

The denominator is more than 3…but notice just how much more:  the expression added to 3 is the same as the original expression, x.

That means we can re-write the continued fraction this way:

We multiply both sides by 3+x and distribute on the left hand side to get:

Were you expecting that?  To evaluate the continued fraction, we have to solve a quadratic equation.  This means that we are going to have to choose a method.  I’m going to vote for completing the square (which I will return to in my next post).  But if you prefer, you can use the quadratic formula.  Either way, you’ll get:

It’s  the positive answer that we want here.  And its nice to see that it falls in the range we expected.

I still like completing the square better.  Before we get to that, here’s one more fun example that will end with a twist.

THE GOLDEN CONTINUED FRACTION:

Let’s call it an exercise (or two):

Show that x must be less than 2 and more than 1.5.

(You can post your reasoning in a comment if you like.)

But again, what if we want the exact value?  We have to notice that once again, the expression we seek is hidden inside the continued fraction. Here it is again:

Look closely – that “something” is the same expression we started with.  It’s x!

So we can re-write the original equation:

And if we multiply both sides by x:

Or:

We still have to solve this quadratic equation.  But those (both?) of you who have been following along with me might remember that we have seen this equation before.  This was exactly the quadratic equation we landed on when looking for the Golden Ratio.  The one equation answers two seemingly unrelated questions:

1. What is the value of this expression with a continued fraction?

2. What is the aspect ratio of a rectangle from which you can remove a square, leaving behind a smaller rectangle with the same aspect ratio?

We’ll know both of these when we solve that quadratic equation.

(That was my idea of a cliff-hanger ending.)

“I was never any good in sports.  I was always terrified if a tennis  ball would come over  the fence  and land near  me, because I never could  get it over the  fence —  it  usually went about  a  radian off of where it  was supposed to  go.”

                                                                                          Richard Feynman

Before I continue my zealous advocacy for radian measure, I should acknowledge that other than Feynman, I have never seen anyone use radians while making an every-day casual reference to the size of an angle.  Degree measure is more convenient here because it is more familiar.  Familiarity is not a bad thing. Besides, even students who have completed a year of trigonometry and who have memorized their way around the unit circle (π/6, π/4, π/3, π/2…) often struggle when I ask them to draw an angle that is approximately one radian.

Try it yourself to see what I mean.  Draw an angle of approximately one radian.  But no fair converting!  Though you could use the fact that π radians = 180 degrees to figure out what one radian is in degrees, that would evade the purpose of the question.  The goal is to develop an intuitive feel for radian measure. So try to draw a radian without “thinking in degrees”.

[Digression]

Early in the school year, students often ask “how much is a kilogram”?  I know they want an answer that relates kilograms to pounds.  But that kind of conversion factor doesn’t help develop intuitive feel.  I prefer to point out that one kilogram is the mass of a liter of water.  And since all of my students walk around carrying half-liter bottles of water at all times (the hydration generation), they all know exactly what a half-kilogram feels like.

[/digression]

So how do we draw that one-radian angle?  Let’s rephrase that question in edible terms: draw a slice of pizza with crust-length equal to the radius!

Since the arc length is equal to the radius, it must be that the ratio is 1:1.  That makes the central angle one radian.  That’s the angle Feynman was using to describe his errant throw.

Now let’s get rid of the pizza and just look at the angle.  Suppose you increase that angle just a little to pull the crust into a straight line (without changing its length).  You would now have an equilateral triangle.

That tells us something interesting:  one radian is a little less than the angle of an equilateral triangle.  And since we already knew that the three of the angles of an equilateral triangle (in fact,of any triangle) add up to a straight line, it must take a little more than 3 radians to also add up to a straight line.

How much more?  You already know that too:  π radians = 180 degrees. Right. But maybe now you have a little more of that radian feeling.

THIS JUST IN:

I found this on BusinessInsider.com in an article by Walter Hickey.

Nice.

Whether we measure a right angle to be 90 degrees or 100 grads, either way we are adopting an arbitrary scale.  But when we say that its measure is π/2 radians, we are using a system that is not arbitrary at all.  It is based on a geometric comparison that works a lot like an aspect ratio.

As we said earlier, the aspect ratio of a rectangle is the ratio of length to width.  Intuitively, it is a measure of the “rectangularity”.  Long skinny rectangles have high aspect ratios.  Squares have aspect ratio L/W = 1.

One important thing to understand about aspect ratios: they don’t tell you anything about the size of the rectangle.  These two rectangles both have the same aspect ratio (2.5) though one is clearly bigger:

Aspect ratios tell you about the shape, not the size.

Also, as long as you measure the length and width with the same units, the aspect ratio is “dimensionless”.  For a given rectangle, you get the same aspect ratio whether you measure your length and width in inches, feet, yards, miles…it doesn’t matter, as long as you use the same units for both measurements.

 Onward to Angle Measurement

Here again are a collection of slices all cut from the same pizza but with different central angles:

And here’s a critical fact to notice about these slices: for pizza of a given radius, the bigger the angle, the more crust you get.  (Many of my mathematical insights involve food. Why is that?)

The crust length is better known as “arc length”.  And now we can define a kind of aspect ratio.  Instead of length-to-width, let’s base this aspect ratio on the arc length and the radius.

The arc length-to-radius ratio is a natural and completely non-arbitrary way to measure the angles.  All of the slices above have the same radius.  So the biggest arc length-to-radius ratio is found on the right where the crust is longest.  And that slice has the biggest central angle.

For example, suppose you cut two slices from a pizza with a radius of 12 inches, one with 6 inches of crust and the other with 9 inches of crust.

 We can define the measure of the central angle as the Angle Aspect Ratio.

For the smaller piece…

Angle Aspect Ratio = Arc Length / Radius = 6inches / 12 inches = 1/2.

And for the larger piece…

Angle Aspect Ratio = Arc Length / Radius = 9inches / 12 inches = 3/4.

As expected, the larger Angle Aspect Ratio is associated with the larger central angle.  You got more crust per radius with that angle.

Also, just like aspect ratios for rectangles, it’s the shape and not the size that matters. These two slices have the same angular aspect ratio.

The bigger slice has more crust but the crust-to-radius ratio is the same. So both of these angles have the same measure:

 And yes, the real name for this system is called “radian measure” (and not “angle aspect ratio”, alas).

In this system, the size of a right angle is not an arbitrary 90 degrees or 100 grads.  Instead, it is the ratio of the arc length to the radius.  But we can figure out that value.  We know a full circle has a circumference of 2πr.  So the arc length of a quarter circle must be 2πr ÷ 4 =πr/2.

Then, to find the radian measure, we calculate the “angle aspect ratio” (as I stubbornly call it):

And now that we know that a right angle measures π/2 radians, we can also say that

π radians = 180 degrees.

That’s a useful fact if you want to convert back and forth from degrees to radians.  But if all you know is that conversion factor, then you have missed the point. I know that some of my students think of radians the way they think of the metric system: another unfamiliar system you have to learn because math and science teachers insist on it.  But seriously, mathematicians are as lazy as anyone else.  They would never have adopted the system of radian measure if it didn’t have advantages over the more commonly used degree measure.  Some of these advantages don’t show up until you are studying physics and calculus.  But some of them can be seen sooner than that.  Stay tuned…

If you have been following my recent posts, you may now be waiting for an impassioned defense of “completing the square”.  It’s coming soon, with pictures (of course).  But talking about the aspect ratio of a rectangle got me thinking about other ratios that show up in geometry. In particular, I want to look at what we might call the aspect ratio of an angle.  This will lead us to a natural way of describing the size of an angle, one that is less arbitrary than the degree system.  So I have interrupted the regularly scheduled digression for a different digression.

Measuring Angles the Familiar Way

When two rays intersect, we say that they form an angle.  For example, the two rays could be cut along different radii of a pizza, intersecting at the center of the pie.  Depending on how you make your cuts, you will get different sizes for your central angle.  If you are hungrier, you cut a larger central angle.

Since angles come in different sizes, we need to have a system for measuring them.  And of course, we have a system that you have known forever.  We call a full circle 360 degrees.  We call a u-turn a “180”, short for 180 degrees.  We call the central angle of a quarter of a pizza a 90-degree angle.  That is also the measure of the angle you find in the corner of every rectangle.  It’s such a familiar system that you may not even realize that it is completely arbitrary.  Who chose 360 as the magic number for a full circle?  (I believe it goes back to the ancient Sumerians, but I haven’t even checked Wikipedia.)  My point is that we didn’t have to do it this way (and we don’t always).

Another way we could measure angles

I’m just saying that this would work too:

Let’s describe the size of an angle by comparing it to a right angle, defining the measure of each angle as a percent of the measure of a right angle.  So for example, the angle made by the diagonal of a square is half the size of a right angle.  You are used to calling that a 45 degree angle, but in our new system, that would be an angle measure of 50 — the diagonal makes 50% of a right angle.

Here are some fun facts about our new system:

1. A right angle has measure of 100. (It is 100% of a right angle!)

2. A full rotation has measure 400. (Cut a pizza into 4 quarters.  The four right angles add up to a complete circle.

3. The measures of the angles of a triangle still add up to the same as the measure of a straight line.  They each have a total measure of 200 in this system.

4. Equilateral triangles have 3 angles with the same measure: 200/3 = 66.666…

This seems arbitrary and unfamiliar – compared to our current system which is arbitrary but at least familiar.  But here’s one other fun fact about our new system:

5.  It isn’t new at all!  It’s an existing system.  When you express an angle as a percent of a right angle, you are measuring the angle in “gradians” or “grads”.  This a real thing. It may even be one of the modes on your calculator (but no one ever uses it).

I’ve read that gradians were used in navigation but I have never seen it done.  To me, it feels like a quirk of history that we chose one arbitrary system over another.  There is, however, another way to measure the size of an angle that is not arbitrary at all.  It is a natural way to describe different angles using ratios in a manner much like the way they are used to describe rectangles.  This system has a real name: it’s called “radian measure” (and your calculator has a mode for this as well).  But we can also think of it as the “Angular Aspect Ratio”.   I’ll describe how it works in my next post.

These may all be digressions, but (as I reassure my students all the time), stay with me.  I’m heading somewhere with all of this.  For now, let’s just keep going.

Here is a rectangle:

And, yes, in Your First Book of Shapes or its equivalent, that was the shape on the “Square” page.  But then in geometry class, you learned that the squares are a subset of the rectangles.  They just happen to have equal length and width.  Still, when I say “picture a rectangle”,  you probably don’t picture a square.  So I’ll try again.

Here is a rectangle:

OK, that is surely a rectangle and not a square.  But is it what you picture when I say “rectangle”?  I’m guessing that my rectangle is skinnier than the one in your mind.  Some rectangles are more “rectangular-y” than others.  We could say they have higher “rectangularity”.  But is there a way to put a number on that?  Actually, there is.  We can use ratios.

Ratios are perfect for this job.  A ratio is a comparison using division.  To find the ratio of A to B, we calculate A÷B.  The answer tells us how many times bigger A is than B.

So let’s define the “Rectangularity” of a rectangle as the ratio of its length to its width.  In that case, my first rectangle had rectangularity of 1 which made it a square.  And my second rectangle had rectangularity of 12.  Its length was 12 times as great as its width.

We can keep calling this ratio “rectangularity”, a name that I made up, but in fact it already has a name: the length-to-width ratio of a rectangle is called its “aspect ratio”.    And in classical design, there is an aspect ratio that is considered ideal.  It just looks right: not too square-y, not too rectangular-y …just right.    It is called the Golden Ratio.  You can find tons of information about  it on-line so I won’t try to replicate it all here.  I just want to look at one interesting feature of a golden rectangle and show how we can use that feature to calculate the Golden Ratio.

Start with a Golden Rectangle…

It looks nice.  But here’s the interesting property.

Slice off a square on one end…that little rectangle that remains is also a golden rectangle.  And yes, if you slice off the end square of this little rectangle, you get another even littler golden rectangle.

Repeat as many times as you like to produce an endless stream of ever-smaller golden rectangles.

Let’s start again.  Suppose the width of the rectangle = 1 and the length = x.

Since the ratio  x/1=x, x must also be the value of the golden ratio.  But what is that value?

Well, for the little rectangle, the length is 1 and the width is x-1.  So that rectangle has an aspect ratio of 1/(x-1).  But that aspect ratio is the same as the aspect ratio of the bigger rectangle we started with.  We can write:

To find the value of the golden ratio, we just have to solve that equation.  When you cross-multiply, you get:

x(x-1) = 1   

You can distribute to get:

x² – x = 1

But now what?  If you use trial and error with a calculator, you will soon find that the golden ratio is a little more than 1.6.  But if you want an exact solution, you need to know how to handle quadratic equations.

And that’s what I really want to talk about.  Quadratic equations pop up in physics.  Not every day, but occasionally.  And they usually can’t be factored.  (Neither can the one we have here.)  My students deal with them a variety of ways.  Some grab their TI89s and let the calculator do the work.   Some of them  use the quadratic formula.  Almost nobody “completes the square”.

I admit that I used to make fun of completing the square as a classic piece of cook-book math – all procedure, no understanding.  But I think I was wrong about that.  I wasn’t picturing the procedure geometrically.  And, as I have mentioned in a few other posts, it’s better with pictures.  I’ll explain in the next post.

In my last post, we saw how taking apart an area in different ways can lead to interesting results.  Let’s do that again.

Here is the square with length (a + b):

(When we looked at binomial squares, I used x and y.  This time, I’m using a and b.  You’ll see why soon.)

Below, I have broken up the square two different ways.  On the left, you see the familiar shapes that we used to derive the formula for the square of a binomial.  And on the right, you see a square surrounded by four identical right triangles.

This gives us two different ways to express the same area.  On the left, we have:

Area = (a + b)² = a² + 2ab + b²

On the right, we have one tilted square in the middle with side c, and 4 right triangles, each with a and b as their base and height.  We can add up their areas to find:

Area = (a + b)² = c² + 4 × ½ × a × b = c² + 2ab

But those two areas are equal.  They are two different ways of chopping up the same square.  That means…

a² + 2ab + b² = c² + 2ab

And if we subtract 2ab from both sides, we get a pretty well known result.

                           a² + b² = c²

where a and b are the legs and c is the hypotenuse  of a right triangle.

We use that theorem all the time.  Again, better with pictures.

All of these posts have been about using pictures to get an improved understanding of what the algebra is telling us.  These are ideas that I have been kicking around for a while so I thought I would share.  But they are leading up to something I’ll write about in the next post.  And I’ll reveal what got me started down this path again this year.

…of two squares.

Suppose we start with a square with side x and remove a smaller square with side y.

The remaining area (shown in blue) is literally “the difference of two squares”.

We can find its area by subtracting the little square from the big one to get:

Area = x² – y²

But we can also find the area another way.  Let’s cut things up and move them around.

As you can see, the area we were looking for is also the area of a rectangle.  The length is (x + y) and the width is (x – y).  That gives us a new formula for this area:

Area = (x + y)(x – y)

But we are talking about the same area both times.  So what we have now is a geometric reason to believe that the difference of two squares can be factored:

                                               x² – y² = (x + y)(x – y)

How important is this?  Hmm.  Within the context of high school math (and SAT math), it is apparently one of the most important factoring facts that there is.  In physics class, I can only think of one setting where we used this. (We were deriving a rule about velocities before and after an elastic collision, in case you were wondering.)

The math we teach should either be useful or interesting.  To me, the difference of two squares is more interesting when we use pictures.  And the idea of carving up the same area two different ways to see what you learn can be very powerful and lead to unquestionably important results.  More about this in the next post.

Well, I hope that the pictures in my last post changed the way you look at the square of a binomial.  And I am sure that I know what you are thinking now:

“What about binomials, cubed?”

We can figure this out algebraically. You may be inspired to see that:

(x + y)³ = (x + y)(x + y)² = (x + y)(x² + 2xy + y²)

And then we distribute:

(x + y)(x² + 2xy + y²) =

                   x(x² + 2xy + y²) +  y(x² + 2xy + y²) =

                                        x³ +2x²y + xy² + x²y + 2xy² + y³

And then you group the common terms to discover the rule for the cube of a binomial.

(x + y)³ = x³ + 3x²y +  3xy² + y³

Let me just say that you have a rare appreciation for algebra if that equation by itself stirs you.  And I would not be shocked to find that you skipped over the algebra that led to it.   But once again, it’s better with pictures.

This time, we build a cube with each edge x + y units long:

Then, we take that cube apart and see what we have:

Let’s take inventory.  The big cube we started with has been broken up into the following collection:

• A white cube with edge length x and volume x³
• A red cube with edge length y and volume y³
• 3 green rectangular slabs, dimensions x by x by y, with volume x²y
• 3 skinny blue rectangular solids, dimensions y by y by x, with volume xy²

But the volume of the collection has to add up to the volume of the big cube we started with.

That means:  (x + y)³ = x³ + 3x²y +  3xy² + y³ ! 

The 3-d picture makes this equation worthy of an exclamation point. The picture helps you to “see” the equation.  That can also work the other way around.  Let’s consider a 4-dimensional “hypercube” with edges that are (x + y).  I can’t picture those.  But I can still get some insight about them from the algebraic approach.  I’ll skip the steps this time and go right to the result:

(x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

Even though I can’t picture a 4-dimensional cube, I think I know what happens when you break it into pieces: you get 1 big hypercube, 1 smaller hyper cube and a variety of hyper-rectangular solids.  You can predict the dimensions and the number of each type from the equation above.  So I guess this time, it’s better with equations.

(The graphics in this post were created in Google Sketch-up by my daughter.)

Let’s start with a silly question about math vocabulary:

Why do some powers have special names?

The expression “ 3⁵ ” means “multiply 3 by itself 5 times”:   3⁵=3×3×3×3×3.  I’m not really worried about how to calculate this right now.  I just want to agree that we call it “three to the fifth”.   And raising to the fifth power doesn’t have any other special name.

And when we talk about x⁷ , we say “x to the seventh”.  Again, no special name.

But there are two powers that have additional names.  When we talk about say, 5², we most often call it “5 squared”.    Raising to the second power is called “squaring”.  Raising to the third power is called “cubing”.  And , of course, you knew that.   But it is easy to overlook why these (and only these) powers have these additional names.  The additional names have geometric meaning.

• When you raise a number to the second power, you are calculating the area of the square with a side of that length.  So we call it “squaring”.
• When you raise a number to the third power, you are calculating the volume of the cube with an edge of that length.  So we call it “cubing”.
• If we lived in 4 spatial dimensions, I bet we would have a name for raising things to the fourth power as well.

It is easy to overlook the geometric meanings of squaring and cubing.  I know this because of how my students respond when we talk about FOIL-ing to square a binomial.  The geometric meaning always seems to catch them by surprise.  But it is usually a happy discovery.

 CURSES! FOILed  AGAIN

For those of you who haven’t seen it in a while, I’ll review.  FOIL is a mnemonic device used to help students remember how to multiply binomials.  It is the result of distributing multiplication over addition multiple times.  You can use it to square binomials.

You start with an expression such as: (x + y)²

You re-write it:  (x + y)(x + y)  

Now, think of that first term as the multiplier and think of the second term as the sum over which multiplication is distributed.  You get:

(x + y)x + (x + y)y

Then you can distribute each of those as well.  That leads you to: x² + xy + xy + y²

Before we combine the middle two terms, note that there are 4 pairings.  That’s where the mnemonic FOIL comes in.  You get the pairs by multiplying the FIRST terms, the OUTER terms, the INNER terms and the LAST terms.

I don’t have a problem with this mnemonic itself.  It’s kind of robotic, but I understand that you have to make certain processes automatic so that you can get to the next step.  I wouldn’t want my students to have to go back to the distribution property every time they see (x + y)².   In fact, I don’t want them to have to foil it either.  I want them to know that (x + y)² = x² + 2xy + y² not because they have memorized it but rather because they can picture it!

THE GEOMETRIC MEANING OF (x + y)²

We call it “squaring” because it gives us the area of the square.

So (x + y)² is the area of the square with length (x + y).  Now, let’s draw some pictures.

Here is a line segment with a length of x + y:

And here is the square with a side that has that same length:

The area of that square is certainly (x + y)².

But what if we break that square into smaller regions?

The picture tells the story in a more intuitive and memorable way than foiling ever could.  We are clearly looking at a big square (with area = x²), a little square (with area = y²), and two identical rectangles (each with area = xy).  This is the diagram that goes with the rule for binomial squares:

(x + y)² = x² + 2xy + y²

But it’s better with pictures.

Next post — higher dimensions.

And then x² – y².   Spoiler: it really is the difference of two squares.